量子アニーリングで組み合わせ最適化問題を解く

はじめに

この記事では、以下の内容について解説します。

• D-Waveマシンを使うための環境構築
• PythonでD-Waveマシンを動かす
• 量子アニーリングを用いて、巡回セールスマン問題を解く

量子コンピュータ

解説に入る前に、量子コンピュータの方式について触れておきたいと思います。
量子コンピュータには大きく二つの方式があります。
一つは量子ゲート方式、もう一つが今回使用する量子アニーリング方式です。

量子ゲート方式

量子ゲート方式は、古典コンピュータの論理ゲートの代わりに、量子ゲートを使って計算を行います。一般的に量子コンピュータというと、この量子ゲート方式のことを指していることが多いです。量子ゲート方式は、量子回路を柔軟に構成できるため、解ける問題が限られていない汎用的な量子コンピュータで、古典コンピュータよりも高速に解くアルゴリズムが開発されており、暗号解読の手法として「ショアのアルゴリズム」が知られています。一方で、量子ゲート方式はノイズの影響を受けやすく、量子ビットにエラーが発生しやすいという課題もあります。また、ハードウェア製造が非常に難しく、大規模な数の量子ビットの実現はまだまだ先と言えるでしょう。現在は、Googleの「Sycamore」やIBMの「IBM Q」などを中心に研究開発が進められています。

量子アニーリング方式

量子アニーリング方式は、高温に熱した金属を徐々に冷やすと構造が安定する「焼きなまし法」を応用して、計算を行います。組み合わせ最適化問題を解くのに特化しています。構造がシンプルなため、ハードウェア開発がしやすく、量子ビットの数も大規模にすることができます。ただ、量子アニーリング方式では、イジングモデルという数式を用いるため、実際に解く問題をイジングモデルに落とし込む必要があります。2011年には、D-Wave Systemsが世界初の商用量子コンピュータを発表し、大学の応用研究や産業分野で既に活用されています。NECも2023年の実用化に向けて研究開発を進めています。

実行環境の構築

今回は、D-Wave Systemsの量子アニーリングマシンを使用し、組み合わせ最適化問題を解いていきたいと思います。まずは、量子コンピュータを使うために、D-Wave Leapのアカウントを作成しましょう。下記のリンクからアカウントを作成してください。

D-Wave Leap

必要事項を入力して、Sing Upすれば、登録確認のメールが届くはずです。

登録出来たら、先ほどのページからログインしましょう。
ログインすると下記のようなダッシュボードがでてきます。

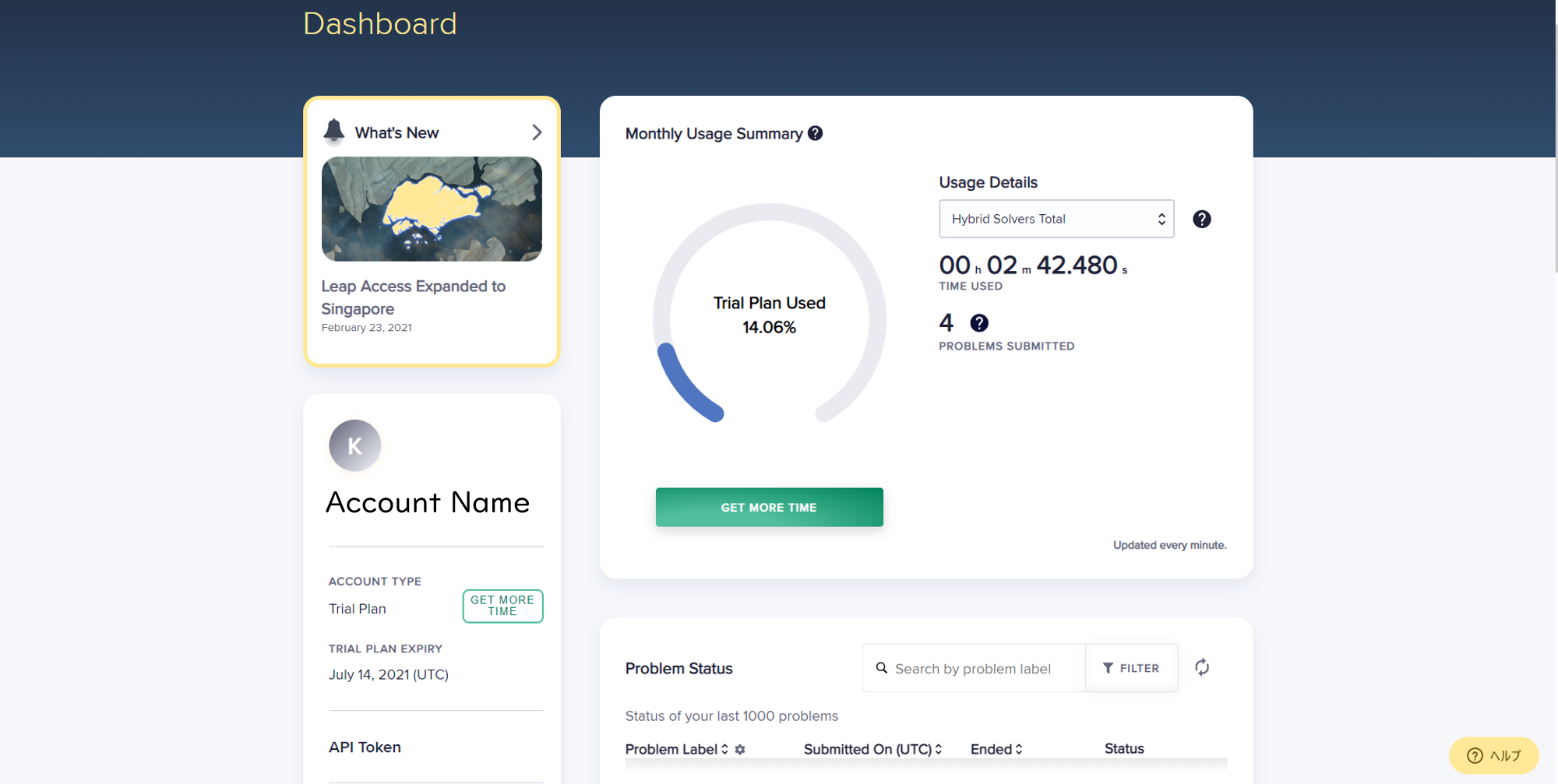
ダッシュボードでは、D-Waveマシンについて、様々な情報を見ることができますが、Monthly Usage Summaryでは、D-Waveマシンの実行時間を確認することができます。

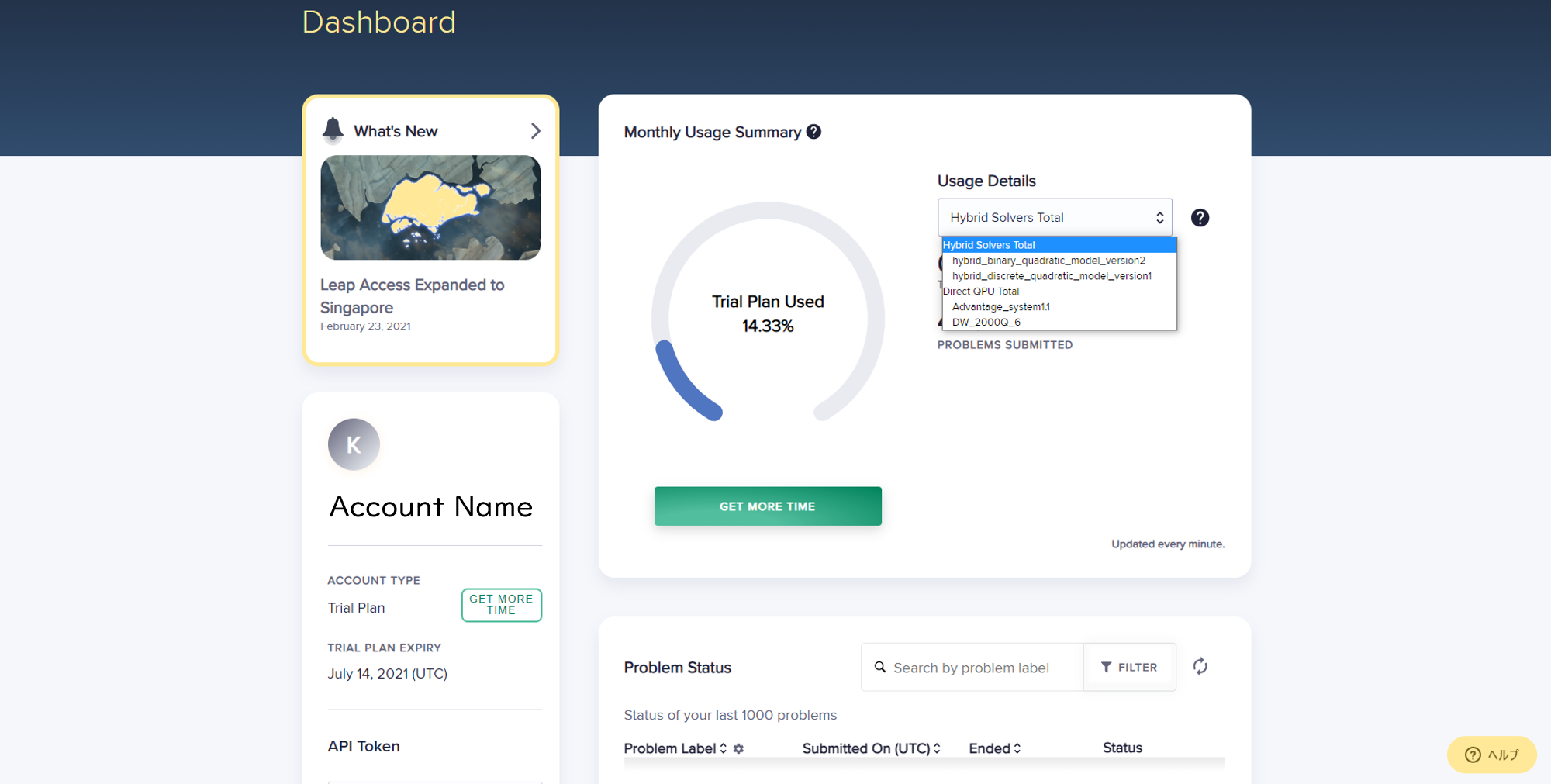
また、Usage Detailsのセレクトボックスを変更することで、各ソルバーやQPUの実行時間を見ることができます。

例えば、DW_2000Q_6を選択すると、実行時間の他に、TIME AVAILABLEというものが出てきます。これはD-Waveマシンの残りの実行可能時間で、新たにアカウントを作った方は1分間のTIME AVAILABLEがあるかと思います。つまり、1分間は無料で、DW_2000Q_6を使わしてくれるということです。1分間しか使えないのかと思いますが、1回あたりの実行速度はかなり短いので、全然心配ありません。ちなみに、EST. PROBLEMS REMAININGが残りの実行回数だと思ってください。

画面左のメニューでアカウント情報を見ることができますが、そこで、API Tokenがあるかと思います。このAPI Tokenは後ほど使用するので、コピーしておいてください。

D-Wave Ocean SDK

D-Waveマシンが使えるようになったので、実際に動かしてみましょう。D-Waveマシンを動かすためには、D-Wave Ocean SDKというものが必要になります。Ocean SDKは、D-Waveの量子コンピューターをプログラミングするためのオープンソースのPythonツールセットです。下記のようにpip installでインストールすることができます。ライブラリの使い方は、このあと実際に問題を解きながら、解説したいと思います。

巡回セールスマン問題とは

今回、D-Waveマシンで、解く問題は「巡回セールスマン問題」になりますが、ここからは問題の概要について紹介します。巡回セールスマン問題は、一般的に次のような文章で説明されます。

より問題のイメージが付きやすいように例題を作りました。

セールスマンがA～Eの5都市を巡回することを考えてみましょう。縦軸（i）が出発地点、横軸（j）が訪問先で、表内に書かれている数値は、出発地点から訪問先への移動距離になります。
ただし、経路を考えるうえで、以下の条件があります。

この時、色々な経路が考えられますが、単純にA→B→C→D→E→Aと巡回したとしましょう。
その時の移動距離は、A（30）→B（10）→C（30）→D（10）→E（40）→Aということになり、総移動距離は120となります。

他の経路も考えてみましょう。

• B（30）→A（50）→D（10）→E（20）→C（10）→B　総移動距離：120
• D（10）→E（20）→B（10）→C（20）→A（50）→D　総移動距離：110
• A（20）→B（20）→E（10）→D（20）→C（20）→A　総移動距離：90

このように、経路によって移動距離が異なります。今回は5都市の巡回なので、考えられる経路の総数は12通りです。都市の数に対する総経路数を一般化すると、(n-1)!/2というように書くことができます。ちなみに、この例題の最適解は、3つ目のA→B→E→D→C→Aになります（巡回順序が同じであれば、始点終点は問いません）。

5都市の巡回であれば解けそうですが、都市の数が10に増えると総経路数は181,440通り、20に増えると6.08×10の16乗通り、30に増えると4.42×10の30乗通りと爆発的に増えていきます。これを現在のコンピュータで解こうとするとスーパーコンピュータであっても、数万年、数億年という時間がかかることが知られています。そこで、量子コンピュータを用いることで、現実的な時間で最適解を求めようと研究が進められているわけです。

巡回セールスマン問題を解く

それでは、実際にD-Waveマシンで、先ほど紹介した例題を解いてみましょう。
使用コードはtraveling _salesman_problem_d-wave.ipynbに公開しています。
以降では、問題を定式化しながら、Pythonコードの解説をします。

インストール

• まず、D-Wave Ocean SDKをインストールしましょう
• インストールしたら、ランタイムをリスタートしてください

定式化

• つづいて、巡回セールスマン問題の定式化を行います
• D-Waveマシンで最適化問題を解く際は、QUBO行列が必要になります
• QUBO行列は、次のように表すことができます

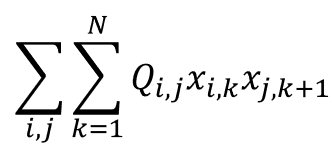
• ここで、Qi,jは出発地点iから訪問先jまでの移動距離を表します
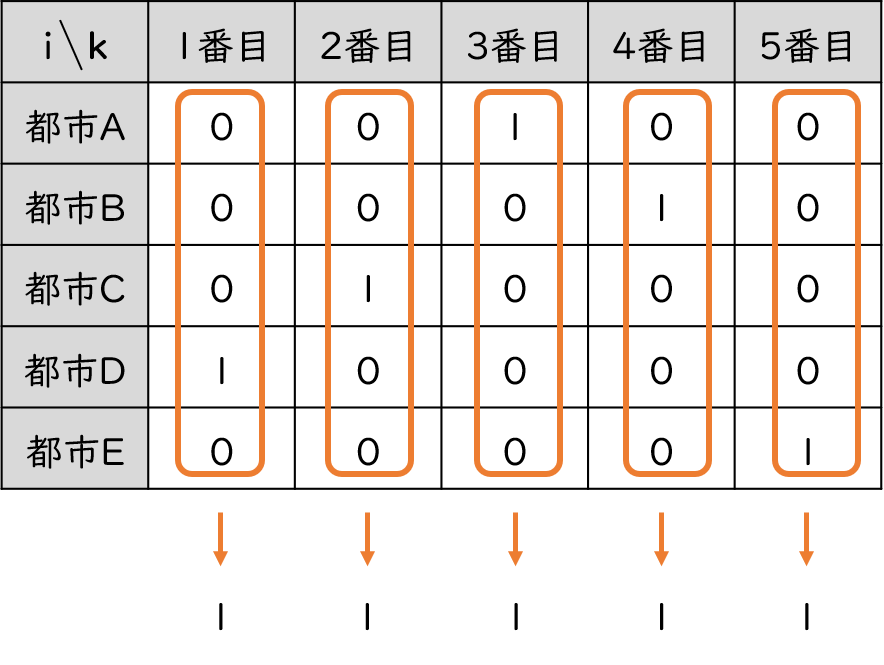
• Xi,k、Xj,k+1は0か1の値で、都市iを時刻kに訪れるか訪れないかを表します
• Xi,k、Xj,k+1を表で表すと、次のようなイメージになります

さて、この問題には、2つの制約条件がありました。

上の表を参考に、制約条件も定式化してみましょう。

・各都市に1回は訪問しなければならない

　　これを表で考えると、各行の合計が１になることを示します。

　　式で表すと次のようになります。

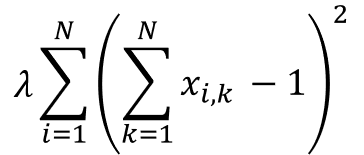
・1度に訪れる都市は1つでなければならない

　　これを表で考えると、各列の合計が1になることを示します。

　　式で表すと次のようになります。

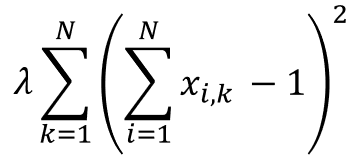
よって、最終的なコスト関数は次のようになります。

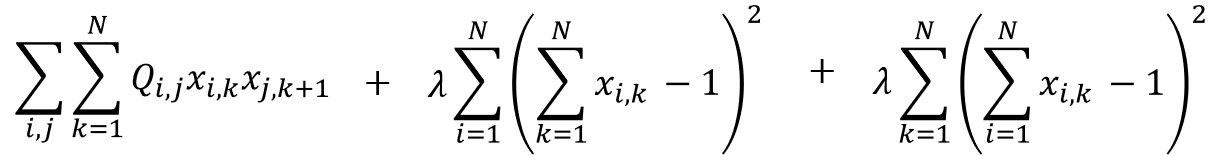
量子アニーリングでは、このコスト関数を最小化することを考えます。制約条件は目的関数（QUBO行列）に足されていますので、プラスの値をとるとコスト関数は大きくなってしまいます。よって、コスト関数が最小になるためには、制約条件が０にならなければなりません。つまり、先ほど解説したように、行方向の合計値と列方向の合計値が1にならなければなりません。

Pythonでは、下記のようにfor文を使って記述しています。

ここでは、pyquboというライブラリを使用して、xを定義しています。
pyquboを使うことで、定式化したコスト関数を展開せずに、問題を解くことができます。

Pythonでは、最終的なコスト関数を下記のように記述しています。

• Placeholder(‘lam’)は、penalty係数を表していて、コスト関数をコンパイルした後もハイパーパラメータとして、変更できるようにしています
• penalty係数を変化させることで、目的関数に対する制約条件の影響力を調整することができます
• Constraintには、先ほど作成した制約条件のconstr_1やconstr_2を渡しています
• Constraintはこれらの制約条件を守っているかをチェックする機能を持っています

ここでは、ハイパーパラメータをコスト関数に渡して、辞書形式のQUBO生成しています。

DWaveSamplerを実行

QUBO行列が作成できたので、D-waveマシンに送って巡回セールスマン問題を解いてみましょう。

まず、tokenとendpointを設定します。
tokenは、先ほど作成したアカウントからコピーしてください。

次に使用するソルバーを定義します。
今回は、DW_2000Q_6を使用します。

つづいて、D-Waveマシンの量子ビット上に問題を埋め込むための準備をします。EmbeddingCompositeで自動的にやってくれるのですが、それゆえに、うまく計算できる時とできないときのムラがあります。問題によって埋め込み方を変更することで、パフォーマンスが劇的に改善されることがあります。

最後に、ソルバーを実行します。num_readsは問題を解く回数で、今回は10回問題を解くように設定しています。このコードを実行すると、カナダにあるD-WaveマシンにQUBO行列が送信され、最適化問題を解いてくれます。num_reads=10なので、数秒もかからずに実行が完了するかと思います。

結果出力

結果は、sampleset.recordで得ることができます。10回計算した結果を下記のように出力できたかと思います。量子アニーリングの結果は最適解とは限らず、実行するたびに毎回出力が異なります。

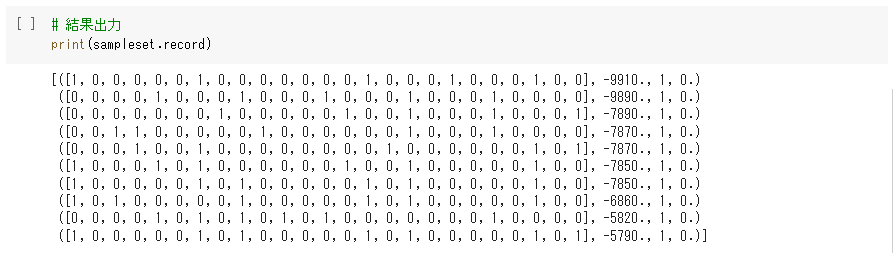
出力結果の見方を解説します。10個のタプルが出力されたと思いますが、一番左の0,1のリストが各都市どのタイミングで訪問するかを表しています。わかりやすく書き下すと、次のようになります。

これは、sampleset.recordの一番最初の結果に対する説明です。0, 1のlistは左から5つずつ分割してみます。そして、各都市、5つの0,1の値を持っていますが、1が立っている位置が、その都市に訪れる順序を示しています。例えば、都市Aは２つ目の値が1なので、2番目に巡回する。都市Bは3つの目値が1なので、3番目に巡回するといった感じです。

そして、sampleset.recordのタプルの左から2番目の要素は、コスト関数値になります。この値が低いほど最適解に近い結果と言えます。

タプルの3つ目は、出力結果の頻度を表します。今回はすべて1でしたが、同じ結果が数回出現した場合は、この値が1より大きくなります。

タプルの4つ目の値は、chain breakの割合になります。基本的に0であれば、問題ありません。複数のビットで1つの変数を表現することがあり、ビット間で強い結合を持たせているのですが、chain breakの割合が0よりも大きいと、ビットの向きがそろっていないことを表しています。つまり、0にするのか1にするのかを迷っているビットがあるということです。

つづいて、各出力結果が、制約条件を守っているかチェックしてみましょう。このチェックは、次のコードで調べることができます。

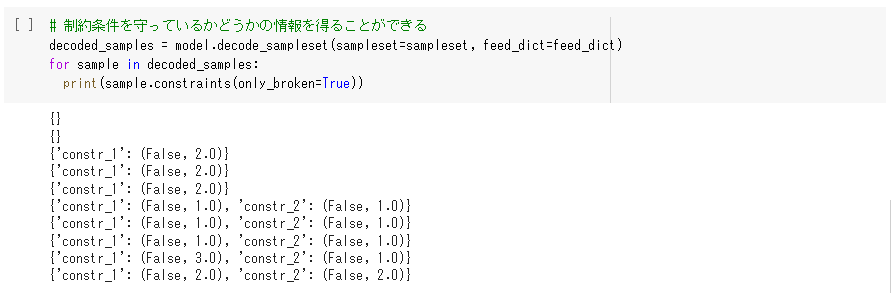
この出力結果をみると、先頭から2つ目までは空のdictが並んでいますが、それ以降のdictは「制約条件：（False, 数値）」という形になっています。この数値は、制約条件を破っている数を示しています。例えば、5番目の結果は、条件1で1つ、条件2で1つ制約を破っていることを表しています。出力結果の前半部分のように、空のdictであれば、制約条件を守った出力結果になっていると言えます。

最後に直感的にわかるように、出力結果を整形してみましょう。コスト関数値が最小の1番目の要素を次のように出力します。

この時、行が都市A～E、列が順序を表しています。そうすると、この結果では、A→B→E→D→C→Aとなりました。各都市間の移動距離はA（20）→B（20）→E（10）→D（20）→C（20）→Aなので、この経路の移動距離は90となって、最適な経路を出力できたことが分かります。

OpenJij

今回は、D-Waveマシンで組み合わせ最適化問題を解きましたが、OpenJijというソフトウェアを使うことでも同様のことができます。OpenJijでは、量子モンテカルロ法という量子アニーリングに相当するシミュレーションで問題を解きます。D-Waveマシンでは計算を実行するごとに料金がかかりますが、OpenJijはプログラムを書いたマシン上で実行するので、ローカルのマシンやGoogle Colabであれば、何度実行しても料金はかかりません。なので、D-Waveマシンで実行する前の練習として使ってもいいかもしれません。

それでは、巡回セールスマン問題をOpenJijでも解いてみましょう。
まずはpip installします。

QUBO行列を作るところまでは、先ほどと一緒なので、ソルバーを定義するところから紹介します。
SQASamplerをインポートして、samplerとして定義します。

あとは、D-Waveマシンで実行した時と同じです。

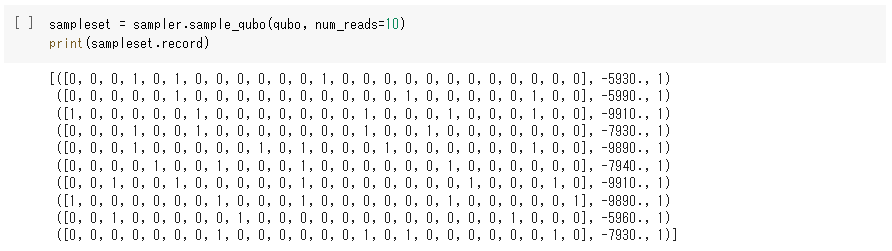
出力結果が出てきました。
コスト関数値が最小の結果を見てみましょう。

D-Waveマシンと同じく、A（20）→B（20）→E（10）→D（20）→C（20）→Aという結果が得られました。

おわりに

今回は、D-Waveマシンを用いて、組み合わせ最適化問題を解いてみました。量子コンピュータというと量子力学から発展したこともあり、敷居が高いイメージがありますが、簡単に量子コンピュータを使用することができるPythonライブラリが公開されており、そのハードルは決して高いものではないと思います。今回は例題として巡回セールスマン問題を使用しましたが、この問題のように定式化することができれば、他の組み合わせ最適化問題も解くことができそうですね。

K.K