はじめに
この記事では、量子アニーリング・イジングマシンで組み合わせ最適化問題を解くためのPythonライブラリAmplifyについて、その使用感やD-WAVE Ocean SDKとの実装上の違いについて紹介します。
Amplifyとは
Amplifyは、株式会社Fixstars Amplifyが提供する量子アニーリング・イジングマシンを実行できるクラウドサービスで、組み合わせ最適化問題を解くための基盤やソフトウェアがそろっています。
利用できる量子アニーリングマシン
Amplifyでは同社が提供するFixstars Amplify Annealing Engineを使うことができます。GPUベースのアニーリングマシンで26万ビット以上の大規模問題の入力と高速実行が可能です。また、その他にもD-Wave 2000Q / Advantage、日立のCMOS Annealing、富士通のDigital Annealer、東芝のSBMを利用することができます。主なマシンスペックは以下に示す通りです。
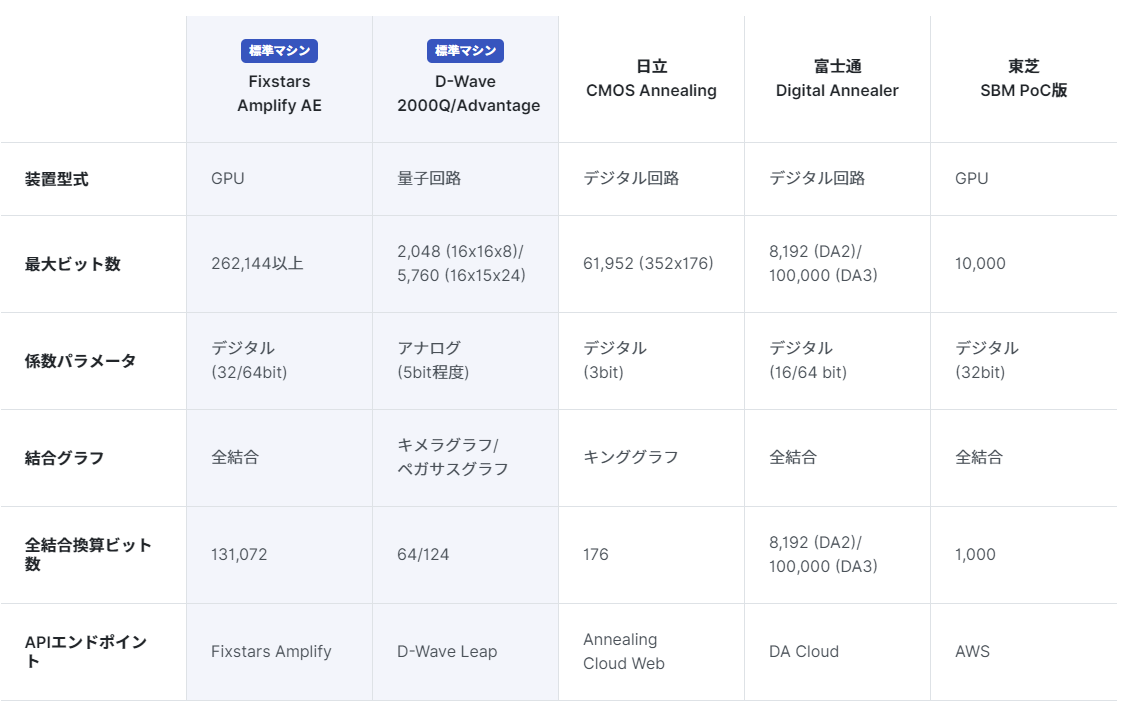
標準マシンとしてAmplify Annealing EngineとD-Wave 2000Q / Advantageを利用することができ、研究・開発の目的であればユーザー登録をすることで無料で利用することができます。
Amplify SDK
Fixstars Amplify SDKがPythonライブラリとして提供されています。コスト関数や制約条件をコードとして記述する上で便利なクラスや関数、アニーリングマシンで最適化を実行するためのインターフェースやソルバーがそろっています。公式のドキュメントでは、プログラミングフローが次のように紹介されており、すべてAmplifyで行うことができます。

以下の図はAmplifyで実装したバイナリ多項式の例です。見てわかるようにシンプルに記述することができるため、ユーザーは問題を解くことに集中できます。

巡回セールスマン問題を解く
今回は以前のブログ記事で取り組んだ巡回セールスマン問題をAmplify AEとAmplify SDKを用いてやってみたいと思います。この記事ではAmplifyでの実装方法に焦点を当てているので、詳しい問題設定については以前のブログ記事を参照してください。
アカウント登録
まず、Amplifyで最適化問題を解くためにトークンを発行する必要があります。こちらのサイトで無料ユーザー登録ができるので、トークンを取得してください。必要事項を入力して登録すると認証コードが送られてきますので、それを入力して登録完了です。
問題設定
それでは、巡回セールスマン問題を解いていきたいと思います。巡回セールスマン問題とは簡単に説明すると、セールスマンがある地点を1回ずつ訪れて出発地点に戻ってくるときに、その移動距離が最小となる経路を求める組み合わせ最適化問題です。
より問題のイメージが付きやすいように例題を作りました。

セールスマンがA~Eの5都市を巡回することを考えてみましょう。縦軸(i)が出発地点、横軸(j)が訪問先で、表内に書かれている数値は、出発地点から訪問先への移動距離になります。
コスト関数は次の通りです。
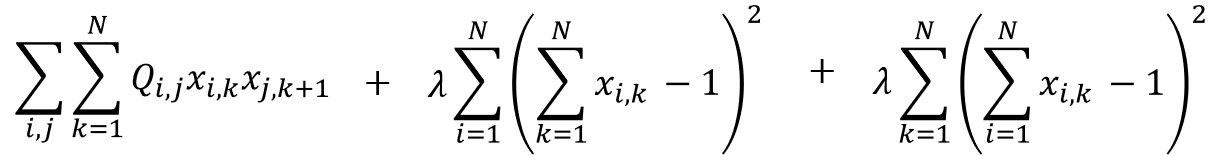
- ここで、Qi,jは出発地点iから訪問先jまでの移動距離を表します
- Xi,k、Xj,k+1は0か1の値で、都市iを時刻kに訪れるか訪れないかを表します
- Xi,k、Xj,k+1を表で表すと、次のようなイメージになります

実装
実装コードはtraveling_salesman_problem_amplify.ipynbにまとめてありますので、こちらと併せてご覧ください。
それでは、実装していきたいと思います。以下のように5都市間の移動距離が分かっており、この時、移動距離が最短となる巡回経路を最適化によって求めたいとします。

次にどの経路を選択するのかを意味する変数を作成します。これは問題設定のところで説明した都市iを時刻kに訪れるか訪れないかを表し0か1の値になります。コードを実行すると、以下のように変数が格納されたBinaryPolyArrayが得られます。
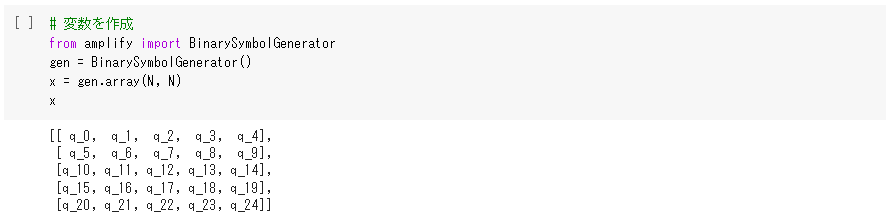
続いて、コスト関数を作成します。
コスト関数は以下のようにeinsum関数を用いることで簡単に実装することができます。

実際、どのようなことがこのコードで計算されているかわかりずらいかと思いますのが、以下の式を計算しています。
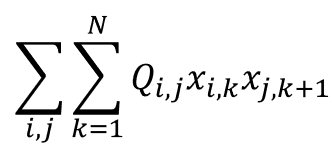
以前、D-WAVEマシンで最適化した際は、PyQUBOで以下のように実装していました。

「都市iから都市jの移動距離 × 都市iのバイナリ変数(時刻k) × 都市jのバイナリ変数(時刻k+1)」という形になっています。つまり、考え得るすべての時刻と都市移動の組み合わせを合計しています。最初の内はfor文で書く方が分かりやすいかもしれませんが、慣れてしまえばAmplifyの方が簡単に書けますね。
コスト関数が実装できたので、再びAmplifyの実装に戻って制約条件を記述したいと思います。制約条件は2つありました。「各都市に1回は訪問しなければならない」と「1度に訪れる都市は1つでなければならない」です。式中では、以下の項が制約条件にあたります。
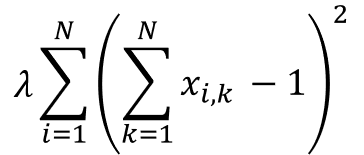
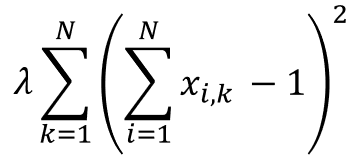
Amplifyでは、ヘルパー関数を使うことで制約条件を定義することができます。

one_hot関数を用いることで、引数に入力した変数の合計値が1になるように制約を課しています。引数にx[n]やx[:, i]が入力されていますが、これは変数xの各行、各列の合計値が1になるよう制限していることを意味しています。
ヘルパー関数はこの他にequal_to(~に等しい)、less_equal(~以下)、greater_equal(~以上)、clamp(~以上かつ~以下)というものがあります。詳しくは公式ドキュメントを参照してください。
ちなみに制約条件は以下のように参照することができます。実際にどのような式になっているのかを確認できるので、この点は便利だと思います。

作成した制約条件をコスト関数に付与します。penalty係数の大きさを変化させることで制約条件の影響力を調整ことができます。

コスト関数が完成したので、実際に量子アニーリングマシンで最適化をしたいと思います。
FixstarsClientのクライアントを以下のように呼び出して、パラメータやトークンの設定を行います。

ここではトークンの他に、タイムアウトの時間を1秒(client.parameters.timeout = 1000)、同じエネルギー値であっても異なる解であれば考慮する(client.parameters.outputs.duplicate = True)を設定しています。この他にも設定できるパラメータがあり、公式ドキュメントに詳細が書かれています。
続いて最適化を実行します。
最適化はコスト関数をソルバーに渡すことで簡単に実行することができます。

結果はresultに格納されており、energyとvaluesを参照することで、エネルギー値と解を得ることができます。
さらに、decode関数を使うことで解を見やすい形に直すことができます。
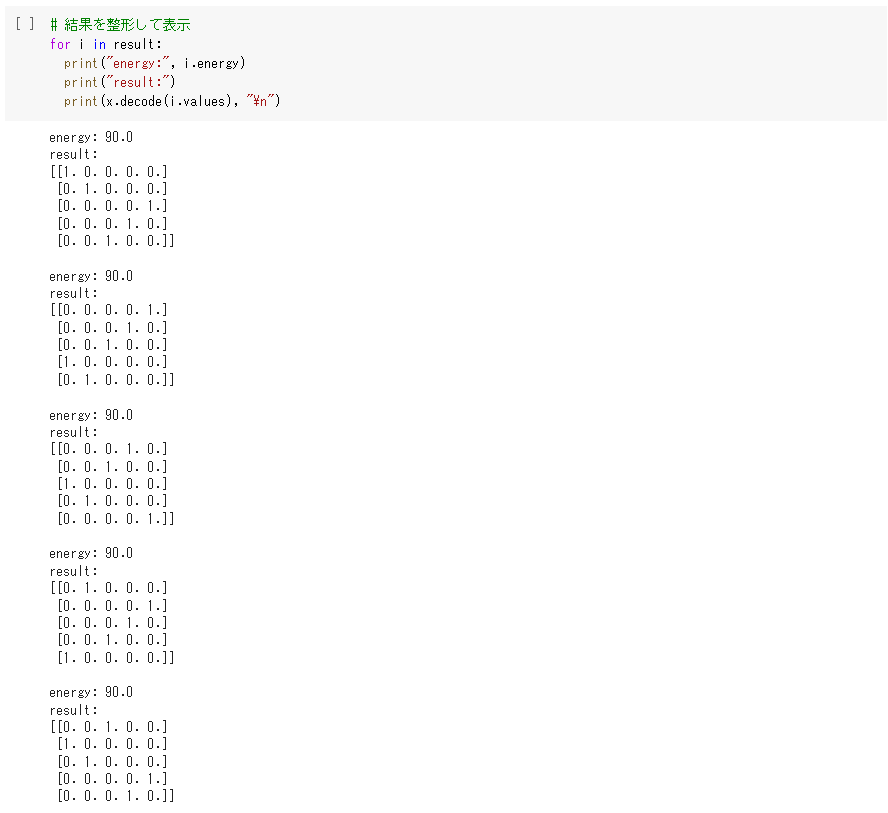
今回はすべての解でエネルギー値が90.0と同じになりましたが、解はいくつかにばらけたようです。この中では1つ目のA(20)→B(20)→E(10)→D(20)→C(20)→Aが最短経路と一致しています。
D-WAVEの量子アニーリングマシンを使って解いた場合とも比較もしてみましょう。
こちらでは10個の解が得られました。

一番エネルギー値が低い1つ目の解を整形して表示してみましょう。Amplify AEと同じくA(20)→B(20)→E(10)→D(20)→C(20)→Aと最短経路を得ることができました。

結果
今回試した巡回セールスマン問題では、Amplify AEでもD-WAVEの量子アニーリングマシンでも最短経路を求めることができましたが、出力された解の数からもわかるようにD-WAVEマシンの方が柔軟性があるかと思います。Amplify AEはGPUベースのアニーリングマシンなので大規模な最適化問題にも対応可能ですが、解の柔軟性ではD-WAVEのほうが優れているのではないか?といった印象です。その一方で、D-WAVEマシンは日によって得られる解にばらつきがあるので安定的に解を求めたい場合には、Amplify AEを使うなど目的によって使い分けたほうがよさそうです。
おわりに
今回は量子アニーリング・イジングマシンで組み合わせ最適化問題を解くためのPythonライブラリAmplifyについて紹介しました。Amplifyの記法には多少の癖がありますが、比較的シンプルにコスト関数を記述できるので、一度慣れてしまえば効率的に実装することができそうです。公式サイトでは、オンラインデモやチュートリアルが公開されていますので、もっと量子アニーリングマシンの使い方や最適化について学びたい方は、ぜひ公式サイトを見ることをお勧めします。
参考
- https://amplify.fixstars.com/ja/
- https://amplify.fixstars.com/ja/docs/index.html
- https://amplify.fixstars.com/ja/demo
(K. K)




