Juliaでk-mean法(4) Word2vec

技術
この記事は約14分で読めます。

はじめに

　これまでのk-means記事

　今回は、Word2vecを用いてk-means法を試してみます。
　Word2vecを使う方法については、別記事「Juliaで日本語Word2vecを使ってみた」をご覧ください。

単語ベクトルと記事の特徴ベクトル

　過去のBOWとTF-IDFでは、単語の出現に応じて記事の特徴ベクトルを定義していました。
　Word2vecは単語をベクトル表現したものです。記事の特徴ベクトルは記事中の単語のベクトルから計算で求めることになります。
　なお、単語ベクトルのWord2vecに対して、文書をベクトル化したDoc2vecという手法もありますが、精度がよくない（個人的にも世間の評価的にも）ので今回は使いません。
　今回は、SWEMという手法を用いて単語ベクトルから記事（文書）のベクトルを作成します。

SWEM

　SWEM＝Simple Word-Embedding-based Methods
　論文では、4つの手法が紹介されていますが、今回は次の３つを使って評価します。

SWEM-aver単語ベクトルの各要素を平均する。よく使われる手法です。
SWEM-max単語ベクトルの各要素の最大値を用いる。
SWEM-concatSWEM-averとSWEM-maxを結合する。ベクトルの要素数は２倍になります。

　一見、処理が大変そうに見えますが、記事中の単語ベクトルがマトリックスで与えられていた場合、それぞれ一行で出来ます。

using Statistics
function average_pooling(vecs_inline)
    mean(vecs_inline, dims=2)
end
function max_pooling(vecs_inline)
    maximum(vecs_inline, dims=2)
end
function concat_average_max_pooling(vecs_inline)
    vcat(mean(vecs_inline, dims=2), maximum(vecs_inline, dims=2))
end

※プログラム全体は、記事の末尾に掲載します。

実行結果

　SWEM-aver、SWEM-max、SWEM-concatの結果です。（太字は、後の「評価」でカテゴリーとクラスターが対応付けられた位置です。）

カテゴリー名Cluster12345678
“local”3717128263026136
“domestic”2248210440542918
“sports”44614035060
“entertainment”130025040125
“science”28130021755
“it”20161150372
“world”6130025101119
“business”332805840412
SWEM-aver
カテゴリー名Cluster12345678
“local”4617362216334388
“domestic”36132135132211859
“sports”25248054491511
“entertainment”37034010631121
“science”156302112220
“it”321502221424
“world”68110172281551
“business”3421348304854
SWEM-max
カテゴリー名Cluster12345678
“local”2231159617472152
“domestic”2126115241193549
“sports”6921443722506
“entertainment”15285235624016
“science”310120420021
“it”2271119613022
“world”25618273201947
“business”11241640548445
SWEM-concat

参考までに、BOWとTF-IDFの結果です。

カテゴリー名Cluster12345678
“local”2618166616459024
“domestic”146246359573622
“sports”4878217022136
“entertainment”1583020224059
“science”6732300337
“it”57346212214
“world”942141019116
“business”2614346224060
BOW
カテゴリー名Cluster12345678
“local”34136818331314
“domestic”10921712019162518
“sports”422129454270
“entertainment”027310191350
“science”021001110370
“it”1034246710
“world”7203461221110
“business”5919141027676
TF-IDF

評価

　まず、各カテゴリーに所属する記事が、どれだけ固まっているか（同じクラスターに集まっているか）を見てみます。すなわち、カテゴリーに所属する記事が８つに分割されたときに、一番多く集まっている箇所の割合を見てみます。

BOW36.5%570/1562
TF-IDF49.0%765/1562
SWEM-aver51.3%802/1562
SWEM-max31.9%499/1562
SWEM-concat31.2%488/1562

　次に、Accuracyを見てみます。そもそもK-means法ではクラスターに分割しますが、クラスターにラベルがついているわけではないので、どのクラスターがどのカテゴリーなのかは別途判断する必要があります。ここでは、次の優先順位でクラスターにカテゴリーを割り当てます。

  1. カテゴリー中の記事の最大数が含まれるクラスター
  2. 同じクラスター内では、カテゴリー中の記事の％が大きい方
  3. それでも決められない場合は、任意に割り当てる

これに基づいて、上記の結果に当てはめると、それぞれのクラスター番号とカテゴリー名の関係は次のようになります。枠内の数値が各手法でのクラスター番号です。

カテゴリー名BOWTF-IDFSWEM-averSWEM-maxSWEM-concat
“local”72884
“domestic”54476
“sports”25351
“entertainment”87163
“science”36627
“it”63735
“world”48212
“business”11548

この表のクラスターがカテゴリの正解だとみなして、Accuracyを計算すると次になります。

BOW29.3%457/1562
TF-IDF36.7%573/1562
SWEM-aver47.2%738/1562
SWEM-max26.0%406/1562
SWEM-concat28.4%443/1562
Accuracy

まとめ

　カテゴリーとクラスターの表を見ただけでは違いが判りにくかったのですが、数値にしてみると

BOW　＜　TF-IDF　＜　SWEM-aver

であることがわかります。

　SWEM-maxやSWEM-concatがBOWよりも低い値になったのは予想外でした。
　SWEM-averは、これまで文書ベクトルを求める際にやっていた単語ベクトルの平均をとるという手法の有効性が確認された形となりました。
　47.2%は低い数値ですが、1562件という少ない記事数で学習なしでk-means法でやったのですからそれなりの数値なのではないでしょうか。（そもそも文書分類の観点からこのカテゴリー分割が妥当であるかどうかという問題もありますが、そこまでは掘り下げません）

参考記事

プログラム全体

いろいろとやってきたので、つぎはぎになりますが、全体のプログラムです。

using JSON

# カレントフォルダにある拡張子が「txt」のファイル名の一覧
files = filter(f -> isfile(f)&&occursin(r".txt$", f), readdir("."))

# 複数回に分けられて取得したjsonデータをマージする
urls = []     # 記事の重複判定用
articles = []   # 重複を覗いた記事
days = Dict{String, Int}()
categories = Dict{String, Int}()
for file in files
    data = JSON.parsefile(file)
    for d in data
        url = d["url"]
        if !(url in urls)
            push!(articles, d)
            day = split(d["datetime"])[1]
            days[day] = get(days, day, 0) + 1
            category = d["category"]
            categories[category] = get(categories, category, 0) + 1
            push!(urls, url)
        end
    end
end
# クレンジング
# 記事文字列からテキストデータを抽出し、形態素解析できるように加工する
#   ・句点で改行させ、不要な空白・空行を除去
function getlines(article::String)
    new_lines = []
    # 形態素解析に長文を渡したり、不要な呼び出しをしないように、文字列を調整
    ## 句点「。」の後で分割する
    lines = split(replace(article, r"。" => "。\n"), "\n")
    for ll in lines
        ## 行頭の空白文字列を削除
        ll = replace(ll, r"^[　 ]+" => "")
        ## 空行は削除
        if length(ll) == 0
            continue
        end
        # 処理済み文字列を格納
        push!(new_lines, ll)
    end
    new_lines
end
# 形態素解析して、語の一覧を返す
using Awabi
# 形態素解析器の設定
## Linux / Mac
#tokenizer = Tokenizer()
## Windows：
#dic = Dict("dicdir" => "C:\\Program Files (x86)\\MeCab\\dic\\ipadic")
#tokenizer = Tokenizer(dic)
## SageMaker Studio Lab
rcfile = "/home/studio-lab-user/mecab/etc/mecabrc"
tokenizer = Tokenizer(rcfile)

function countword(tokenizer, lines)
    # 数え上げ格納領域
    word_counts = Dict{String, Int}()
    doc_counts = Dict{String, Int}()

    # 形態素解析＆数え上げ
    for line in lines
        # 1文を形態素解析
        tokens = tokenize(tokenizer, line)
        new_tokens = []
        for token in tokens
            attr = split(token[2], ",")
            hinsi = attr[1]
            surface = token[1] # 表記
            basic = (attr[7] != "*") ? attr[7] : surface   # 形態素の基本形
            ## 
            if hinsi in ["名詞", "動詞", "形容詞", "副詞"] 
                push!(new_tokens, basic)
            end
        end
        # 形態素数を数え上げ
        for surface in new_tokens
            word_counts[surface] = get(word_counts, surface, 0) + 1
            doc_counts[surface] = 1
        end
    end
    (word_counts, doc_counts)
end
# 単語ベクトルの取得
using Embeddings
const embtable = load_embeddings(FastText_Text{:ja})

# 単語文字列からインデックスを取得するテーブル
const get_word_index = Dict(word=>ii for (ii,word) in enumerate(embtable.vocab))

# 単語文字列をベクトルに変換
function vec(word)
    ind = get_word_index[word]
    emb = embtable.embeddings[:,ind]
    return emb
end
function has_vec(word)
    haskey(get_word_index, word)
end
using Distances
cosine(x,y)=1-cosine_dist(x, y)      # ベクトル間のcos類似度

# 指定ベクトルに最も近い単語文字列をn件表示する
function closest(v, n=20)
    list=[(x,cosine(embtable.embeddings'[x,:], v)) for x in 1:size(embtable.embeddings)[2]]
    topn_idx=sort(list, by = x -> x[2], rev=true)[1:n]
    return [embtable.vocab[a] for (a,_) in topn_idx]
end
using Statistics

# 記事中の単語出現数を表すDictと単語ベクトルから記事のベクトルを計算する
function line2vec(word_count_inline)
    hcat([vec(w) * c for (w, c) in collect(word_count_inline) if has_vec(w)]...)
end

function average_pooling(vecs_inline)
    mean(vecs_inline, dims=2)
end
function max_pooling(vecs_inline)
    maximum(vecs_inline, dims=2)
end
function concat_average_max_pooling(vecs_inline)
    vcat(mean(vecs_inline, dims=2), maximum(vecs_inline, dims=2))
end
# 特徴ベクトルの作成
@elapsed begin
    list_vector = []
    for article in articles
        text = article["detail"]
        lines = getlines(text)

        # wcs=記事ごとの単語と頻度の一覧
        (wcs, dcs) = countword(tokenizer, lines)
        article["word_count"] = wcs

        # それぞれ切り替えて実行        
        push!(list_vector, average_pooling(line2vec(wcs)))
        #push!(list_vector, max_pooling(line2vec(wcs)))
        #push!(list_vector, concat_average_max_pooling(line2vec(wcs)))
    end

    # 行列に変換する. juliaはcolumn-major order
    mat = hcat(list_vector...)
end
# K-meansを使って、カテゴリー数8個のクラスタに分類する
using Distances
using Clustering

n_clusters = 8 #the number of clusters
result = kmeans(mat, n_clusters; maxiter=200, display=:none, distance=CosineDist())
clust_numbers = assignments(result) # get the assignments of points to clusters
# 元のカテゴリーと、クラスタリングの結果を比較する
# カテゴリごとに、各クラスタに含まれる記事数を求める
check_table = Dict([(name, zeros(Int, n_clusters)) for name in keys(categories)])
for (clust_no, article) in zip(clust_numbers, articles)
    category = article["category"]
    check_table[category][clust_no] += 1
end
check_table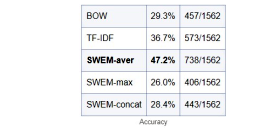

コメント

タイトルとURLをコピーしました